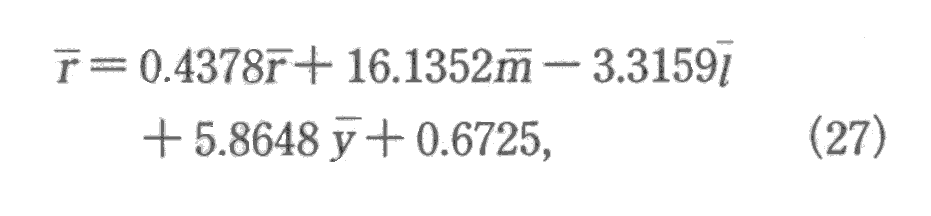単位根検定が,定常,非定常両方の可能性を示したので,前章では定常の場合を扱い,本章では非定常とみなしたときの解析を行う。表2,3で共和分の存在が否定されていたので,(r,m,l,y)のすべての変数を1次差分してVARモデルを作成すればよい。
回帰変数の尤度比検定
前章と同様に,システムモデルを推定する。ただし,r(t)が非定常であるから,R(t) の代わりにr(t)を,または,r(t)の代わりに△r(t)を代入する。表1より,r,mがトレンドを持っていたので,差分変数によるVARモデルは定数のみを持つことになる。次数は最大尤度法規範によりp=2と決定された。△y(t)の回帰において,△r(t−i)を除外することの妥当性を検証するために,尤度比テストを行った。p値は,0.0766となり,△ y(t)の回帰変数△r(t−i)の係数をゼロと置く帰無仮説は10%で棄却され,5%では棄却されない結果となった。しかしながら,r→m→yとr→l→yを識別することを目的としているときに,△y(t)に直接△r(t−i)が混入することは,識別を困難にするので,ここでは△y(t)の回帰変数から△r(t−i)を除外する。
システムモデル
式(1)におけるシステムモデルを式(14)から式(17)と同様に推定する。
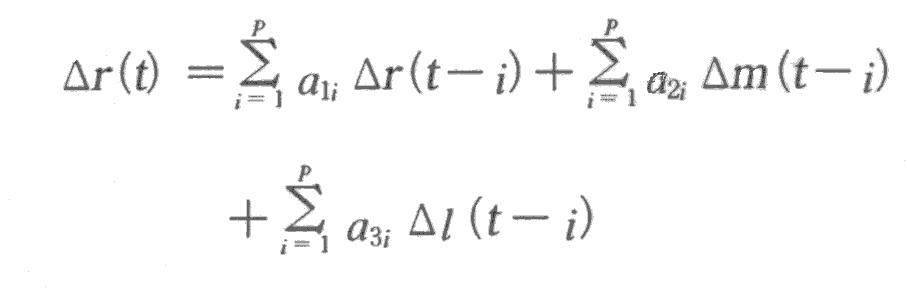
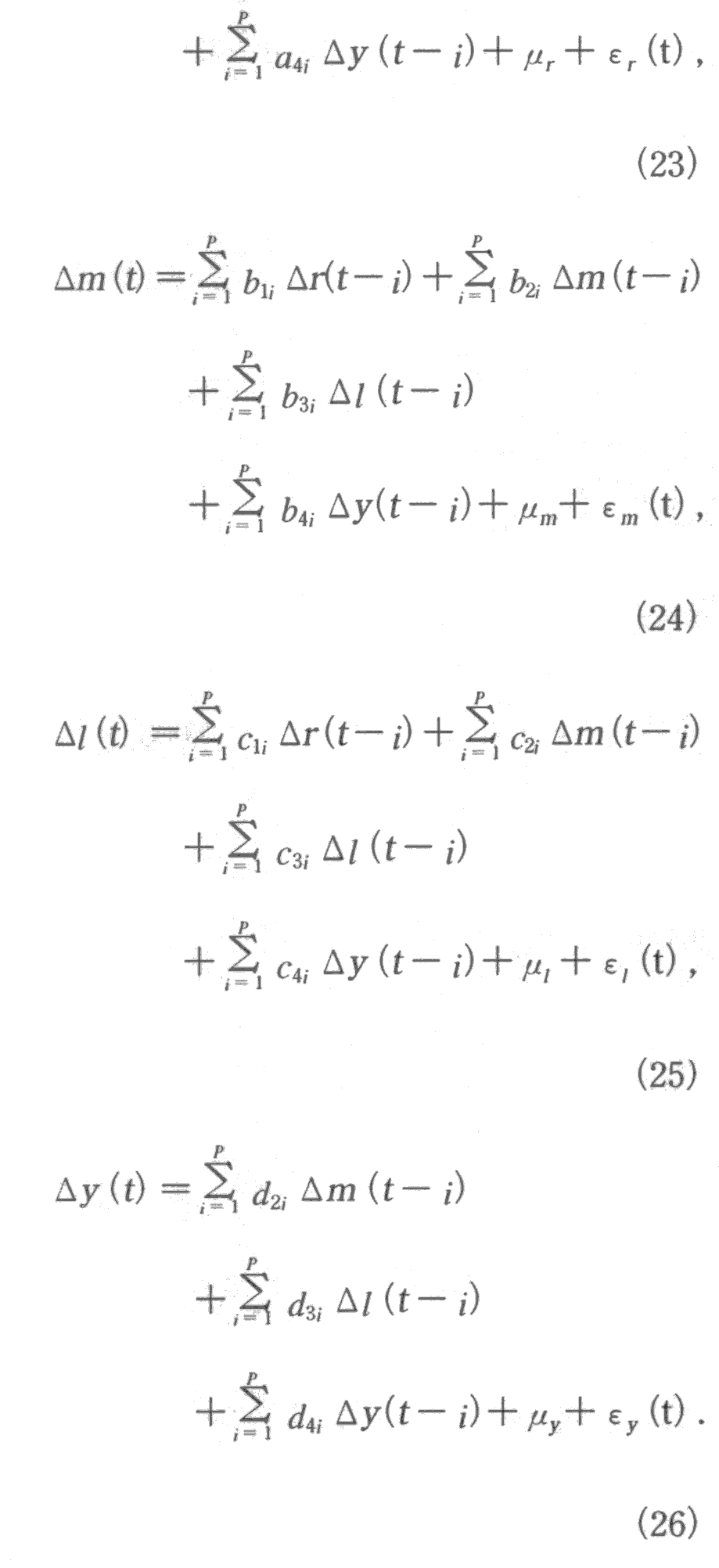
差分過程のインパルス応答を図5に示す。レベル変数のインパルス応答は,累積和を取ることによって得られる。漸近的な貢献度と併せて図6に示す。式(6)を書き直して以下の関係式を得る。