RomerとRomer[4]は金融引締め時のデータだけを抽出し,マネーは産出量に対して影響するが,銀行貸出は経済活動の変化に受動的に反応するにすぎないとしてクレディットビューを否定した。
Ramey[5]は誤差修正モデルを用いて貸付と貨幣量のどちらが算出の変化を適切に予測するかを調べ,マネービューを支持した。
日本のデータを使ってこの問題を検証したものとしては,Romer流のモデルを使った K.Ueda[6],Ramey流のモデルを使った細野 [7],MiyagawaとMorita[8],インパルス応答を用いた畠田[9],銀行貸出とマネーサプライのどちらがGDPの押し下げ効果があるかを調べた原田と茨木[10],その他,多くの研究 がある。最近,中川[11]はGrangerの因果性 とインパルス応答の双方から総合的にこの問題を扱った。(よくサーベイされているので,最近の研究については中川を参照されたい)。 中川はこれまでの研究の多くに見られる欠点 として,m→yの中にm→l→yが含まれていることを指摘し,クレディットビューとみなされるべき分が間違ってマネービューにカウントされているとした。彼はTodaと Yamamoto[12]のモデル化のもとで,弱外生性の概念を導入し,マネーと銀行貸出のモデル式においてインパルス応答を求める際,他の変数からのフィードバックを断ち切って,GDPへの影響を調べ,そのときの
インパルス応答の波形からクレディットビューの優位性を主張した。
本研究では,新しいインパルス応答の手法を提案する。単位根を有するレベル変数を成長率のモデルによって記述し,成長率のインパルス応答の累積和を取ることにより,漸近的なGDP,マネーサプライ,銀行貸出のノンゼロの収束値を得る。これによって,GDPに対する漸近的な貢献度が得られるので,銀行貸出を経由する場合と経由しない場合のマネーからGDPへの経路の識別を評価する可能性を得た。上記中川のインパルス応答の波形から判断するよりもより明確な形で,数値 として経路の識別を行うものである。
2 モデリング
システムモデル
r(t),m(t),l(t)およびy(t)を,t=1,2,・・・における金利,マネーサプライ,銀行貸出,GDPとする。(m,l,y)の各変数をI(1),rをI(0)とする。rが非定常(I(1))な場合は,この章の最後で示される。非定常な(m,l,y)の存在から,考察するモデルは,(△m(t),△l(t),△y(t))を変数として,定常なr(t)によって駆動されるVARモデルで与えられる。ただし,△は△m(t)=m(t)-m(t-1)を意味する差分オペレータである。記述を簡単にするために,新しい変数R(t)≡r(1)+r(2)+・・・+r(t)を導入する。関係式△R(t)≡r(t)を念頭におくと,x(t)=(R(t),m(t),l(t),y(t))'が満たすべきシステムモデルは次式で記述されるものとする:
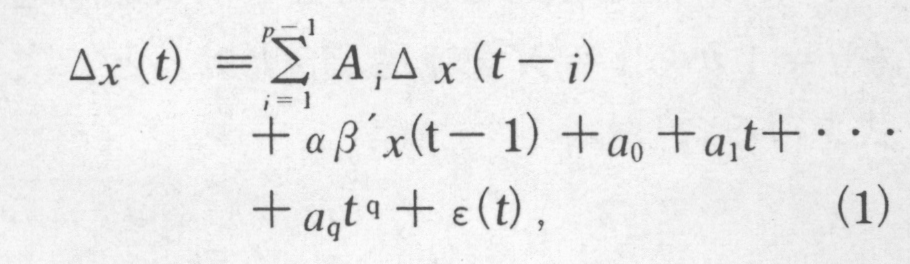
- 2 -