ここで，上式の右辺第２項は，Johansen[18]によって定式化された共和分を表し，は的確なトレンドを，は独立しな４次元の白色雑音系列を表すものとする。

インパルス応答とその漸近挙動
　ｒ (t)ショックを受けたときの△x(t)のインパルス応答を求める。すなわち,上式(1)におけるの第１要素にショックを与えることになる。上式の確定的なトレンドを消去することにより，ゼロ状態のまわりでのインパルス応答を求めることに帰着される。インパルスショックはｔ＝１のみ印加され，かつ，△x(t)が定常であることより，システムの状態量△x(t)および共和分を表す誤差修正項はともにｔ→∞においてゼロに収束する。
　式(1)を同定するとき，残差の共分散行列は一般に対角行列にはならない。Cholesky分解による分散行列の直交変換を導入した。
　△x(t)のインパルス応答に関して時刻１から ｔ まで累積和を取ることにより，x(t)自身のインパルス応答が求まる。ｔ→∞において△x(t)→0およびの性質が成り立つことにより，x(t)の漸近的挙動について次の関係式を得る。

　　

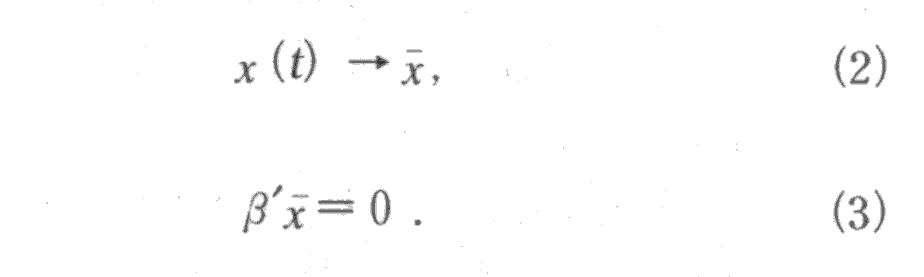
　以上の手続きを実現する。まず，式(1)において，確定的トレンド項を0と置き，と定める。このとき同式の同式の両辺を ｔ＝1 から ｔ＝Ｎ まで足し合わせると，次式を得る。