金利が定常なときは,上記の共和分解析においてr (t) はJohansenのテストから除外された。ここで,r (t) の累積和R(r)≡Σr (t) が関係式△R (t) ≡r (t) を満たしているので,もしR (t) が単位根を持つならば(R,m, l,y)の共和分をチェックする必要性が考えられる。r (t) はトレンド定常であるから,R (t) については時間に関する2乗トレンドのまわりでの単位根検定を要する。モンテカルロ実験によって2乗トレンドを有するADF検定の臨界値を計算し,ADF検定を2乗トレンドの場合に実行すると,R (t) の単位根は棄却されないことが示される(t値−2.71, p値0.42)。計算方法については森田[17]参照。しかしながら,ADF検定の検出力が弱い こと,ERS,KPSSなどの検定方法が2乗ト レンドに対応していないことから,R (t) が定常である可能性が捨てきれない。ここでは R (t) を共和分テストに含めることはしない で,解析を進めることにする。
3.1定常な金利の場合,[1975:1,1997:4]
回帰変数の尤度比検定
我々の目的は,金融政策r (t) (≡△R (t) ) がm (t) とl(t)のチャンネルを経由してどのようにy (t) まで波及して行くかを求める ことである。△y (t) は△y(t−i),△m(t -i)および△l (t−i) によって回帰される。こ こで,r(t-i)は回帰変数から除外する。これは,r(t-i)から△y (t) への直接の影響 を排除して,r (t−i) が2つのチャンネルを経由してのみ△y (t) に働くように設定することを意味する。r(t-i)を△y (t) の回帰変数に含ませるならば,直接の影響r→yと,チャ ンネル経由の影響r→m→yまたはr→l→y とが識別できなくなるから
である。システムモデルの遅れ次数は最大尤度規範によりp=2と決定された。△y (t) の回帰から
r(t−1) とr(t−2)をはずすことの是非を確認する ために,尤度比テストを行った。r(t−i)の 係数をゼロとする帰無仮説のp値は0.3715と なり,帰無仮説を棄却できないという結論を得る。
システムモデル
式(1)におけるシステムモデルを以下のように推定する。ここで,△r (t) ,△m (t) ,および△1 (t) は右辺に線形トレンドを有するものとする。これは,上記の各変数が右辺にトレンドを持ったr(t−i)を回帰変数として抱えているからである。他方,△y (t) はr(t− i)の回帰を含まないので,線形トレンドを右辺に含まないものとする。
なお,変数の順番は金利変数を先頭に持ってきて,(R,m,l,y)としておく。Cholesky分解を用いているので,VARモデルのインパルス応答が変数の順番に影響されるという事実から逃れることはできない。ただし,金利ショックを考えるときは,金利変数を先頭に持ってくる限りは,残りの変数(m,l,y)の順番をどう変えようとも,その後のインパル ス応答に全く影響しないことは簡単な行列計算で確認できる。
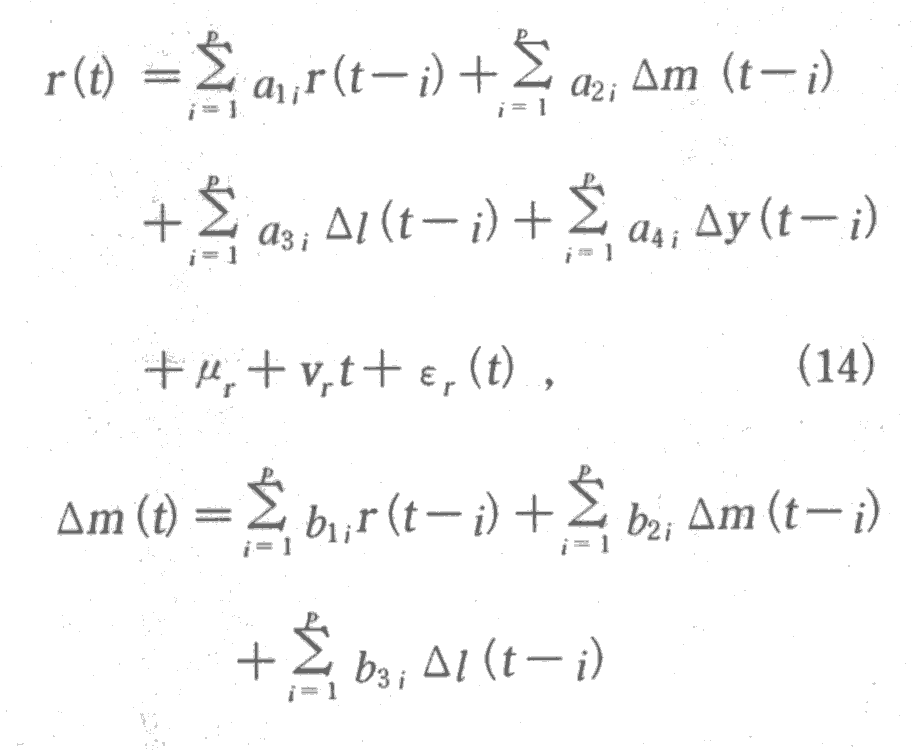
r(t−1) とr(t−2)をはずすことの是非を確認する ために,尤度比テストを行った。r(t−i)の 係数をゼロとする帰無仮説のp値は0.3715と なり,帰無仮説を棄却できないという結論を得る。
システムモデル
式(1)におけるシステムモデルを以下のように推定する。ここで,△r (t) ,△m (t) ,および△1 (t) は右辺に線形トレンドを有するものとする。これは,上記の各変数が右辺にトレンドを持ったr(t−i)を回帰変数として抱えているからである。他方,△y (t) はr(t− i)の回帰を含まないので,線形トレンドを右辺に含まないものとする。
なお,変数の順番は金利変数を先頭に持ってきて,(R,m,l,y)としておく。Cholesky分解を用いているので,VARモデルのインパルス応答が変数の順番に影響されるという事実から逃れることはできない。ただし,金利ショックを考えるときは,金利変数を先頭に持ってくる限りは,残りの変数(m,l,y)の順番をどう変えようとも,その後のインパル ス応答に全く影響しないことは簡単な行列計算で確認できる。
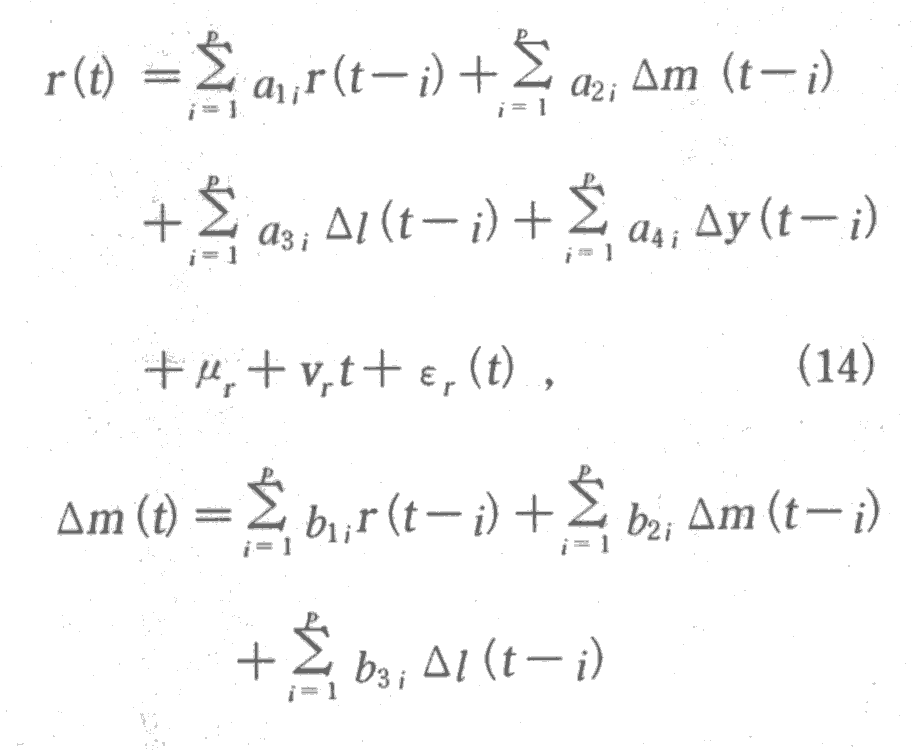
- 8 -